Jason Yuan's Math Blogs

Hello and welcome to my second blog post! I hoped you liked my last one and learned a lot. Today, I want to switch topics to complex numbers. A lot of problems seemingly having nothing to do with complex numbers can be represented using complex numbers either in the complex plane or using generating functions, and it’s really interesting to see how complex numbers can perfectly model certain problems. Let’s look at a problem from the 2015 AMC 12B that uses complex numbers to solve a problem in the x-y plane:

“A bee starts flying from point P_0. She flies 1 inch due east to point P_1​. For j ≥ 1, once the bee reaches point P_j​, she turns 30º counterclockwise and then flies j + 1 inches straight to point P_j+1​. When the bee reaches P_2015​ she is exactly a√b + c√d inches away from P_0​, where a, b, c, and d are positive integers and b and d are not divisible by the square of any prime. What is a + b + c + d?”

When seeing this problem for the first time, one might think to find a pattern that repeats every 12 points, since the bee travels in 12 distinct directions, or maybe even use vectors. While the problem can be solved these ways, there is another neat solution involving complex numbers that I personally think is the best.

First, we can assume P_0 is the origin. Next, we can change the x-y plane into the complex plane, where each point’s (x,y) coordinates corresponds to the complex number x + yi. This is motivated by the fact that rotation by 30 degrees about the origin in the complex plane is very easily done by just multiplying by cis(30º). If we want to find a point that is x units away from a point P in the 30º direction, for example, we just have to add xcis(30º) to a+bi to find the point. This can model all points P_i: if we call cis(30º) x, then P_1 is the point 1 in the complex plane, P_2 is 1 + 2x, P_3 is 1 + 2x + 3x², P_4 is 1 + 2x + 3x² + 4x³, and so on. This is because cis (30a) = cis(30)^a, if you are a little rusty with your complex numbers. 

Thus, the coordinates of P can be represented as:

1 + 2x + 3x2 + 4x3 + … + 2014x2013 + 2015x2014

But how do we find this sum? Well if we call the sum S, we can multiply S by x to get another useful sum:

S = 1 + 2x + 3x2 + 4x3 + … + 2014x2013 + 2015x2014

S • x = 1x + 2x2 + 3x3 + … + 2014x2014 + 2015x2015

Now if we subtract the second sum from the first, we get:

S • (1-x) = 1+ x + x2 + x3 + x4 + … + x2013+x2014 - 2015x2015

The first part is just a geometric series with common ratio x, so we can rewrite as 

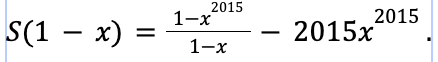
Dividing both sides by (1-x),

x²⁰¹⁵ is equal to x^-1 due to the fact that x^-1 = x¹¹ = x²³ =…=x²⁰¹⁵ since cis(30)¹² = cis(360) = 1 so we can raise to the power of 12 continuously without changing the value.

That’s much nicer. We are trying to find the distance from S to the origin, which is the magnitude of S. Since the magnitude of x is 1, we just have to find the magnitude of

. We just need the magnitude of 1 – x to find the final answer.

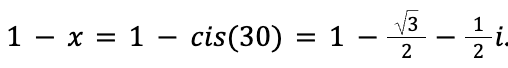
The magnitude of this is just

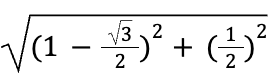
, or

. The magnitude of S is then equal to

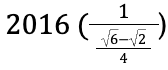
, or 1008√2 + 1008√6. Thus, the answer to the problem is (B) 2024. 

Whew! A lot of calculation in that one. That’s not the important part, though. This was number 25 on the AMC12, and to be honest, using complex numbers made the solution pretty easy for a problem of that caliber. A lot of problems, especially geometry problems, can be simplified using complex numbers, and I hope you learned a lot or honed your instincts detecting these types of problems after reading this!